The accuracy of a machine learning system depends on the complexity of the model that it uses to make predictions, as well as the number of data instances available for training this model. The experiments described in this post are designed to evaluate the performance of three ResNet image classification models, each with a different number of layers. These models were trained using 50,000 images from the CIFAR-10 dataset, but were also trained separately using smaller subsets of the CIFAR-10 dataset.
The CIFAR-10 Dataset

The CIFAR-10 dataset consists of 60,000 low-resolution images. These images are so small (32 pixels on each side) that even a highly complex model can be trained on a single GPU in a matter of hours. Each image in the CIFAR-10 dataset is labeled as a member of one of 10 mutually exclusive classes. The images are split up into a training set (50,000 images) and a test set (10,000 images).
ResNet
Convolutional Neural Nets (CNNs) are very good at solving image classification problems, and the ResNet architecture is a popular type of CNN. I decided to run experiments on three different ResNets, with as few as 8 and as many as 56 layers. I wrote a program that builds, trains, and evaluates a ResNet on the CIFAR-10 dataset using TensorFlow:
github.com/seansoleyman/cifar10-resnet
This program permits training on a subset of the full CIFAR-10 training set. The ResNet architecture can be visualized interactively using TensorBoard. The TensorBoard image below shows a ResNet block with two layers. As an example, ResNet-56 consists of 27 similar blocks stacked one atop the other, plus a few more layers at the top and bottom of the stack. The references at the end of this post provide detailed information about CNNs and ResNets.
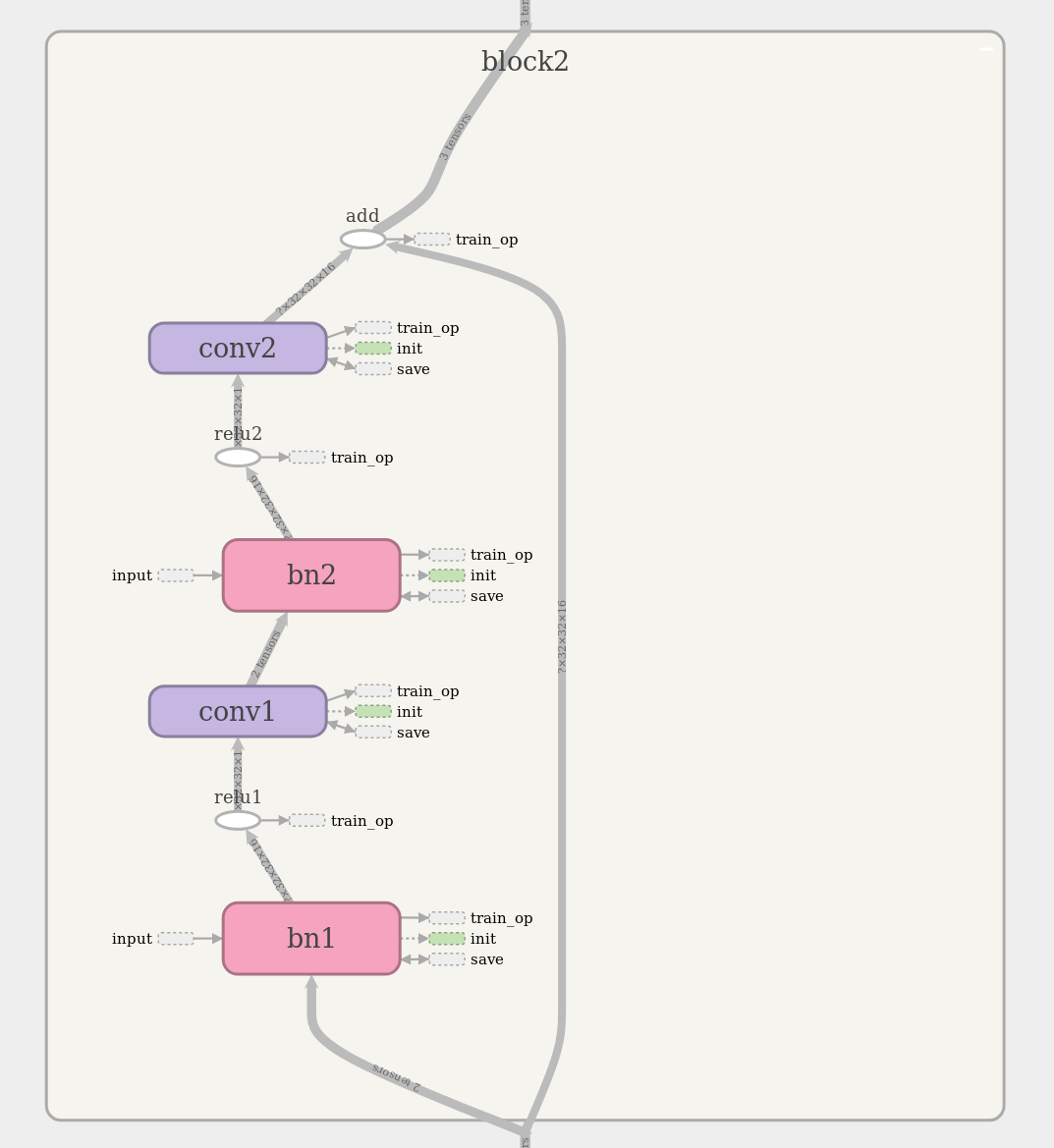
Experimental Observations
Here are the results that were obtained after training three different ResNets on subsets of the CIFAR-10 training set. Each data point represents the test set error rate that was achieved after training the model on a certain number of images. For example, the models on the very left hand side of the graph were trained on just 500 images, and the ones on the right hand side were trained on all 50,000.

Conclusions
Although it is well known that increasing the amount of training data increases the performance of a model, it is interesting that the relationship plotted above follows such a well-defined exponential decay pattern. The error rate appears to approach an asymptotic limit as the amount of training data is increased.
It looks like it would be possible to fit an exponential decay function to the points plotted above. This exponential function could then be used to extrapolate and predict the performance that a model would achieve if more training data were available.
References / Links
- Aurelien Geron, Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems
- Ian Goodfellow and Yoshua Bengio and Aaron Courville, Deep Learning (available online)
- Kaiming He et. al., Deep Residual Learning for Image Recognition
- Kaiming He et. al., Identity Mappings in Deep Residual Networks
- Alex Krizhevsky, Learning Multiple Layers of Features from Tiny Images